2017成都华杯赛备考每日一讲:最优方案
2016-10-27 13:41:58
标签:华杯赛
2017年成都赛区第22届华杯赛初赛即将开考,为了帮助成都赛区华杯赛考生更好的备考初赛,查字典奥数网开始每一日讲的华杯赛备考模式,供参考。
华杯赛每日一讲:最优方案
【最优方案】
例1某工厂每天要生产甲、乙两种产品,按工艺规定,每件甲产品需分别在A、B、C、D四台不同设备上加工2、1、4、0小时;每件乙产品需分别在A、B、C、D四台不同设备上加工2、2、0、4小时。已知A、B、C、D四台设备,每天最多能转动的时间分别是12、8、16、12小时。生产一件甲产品该厂得利润200元,生产一件乙产品得利润300元。问:每天如何安排生产,才能得到最大利润?
(中国台北第一届小学数学竞赛试题)
讲析:设每天生产甲产品a件,乙产品b件。由于设备A的转动时间每天最多为12小时,则有:(2a+2b)不超过12。
又(a+2b)不超过8,
4a不超过16,
4b不超过12。
由以上四个条件知,
当b取1时,a可取1、2、3、4;
当b取2时,a可取1、2、3、4;
当b取3时,a可取1、2。
这样,就是在以上情况下,求利润200a+300b的最大值。可列表如下:
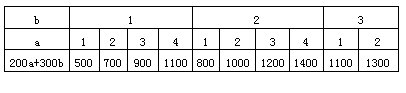
所以,每天安排生产4件甲产品,2件乙产品时,能得到最大利润1400元。


查看全部
来源:查字典奥数网