小学同学如何更有效地学好奥数?
孩子怎么刷题比较有效?
刷题是一个循序渐进的过程,同一个阶段的题目越后面越熟练。现在的模式却是,家长可能基础题20道,然后中档题20道,然后难题20道。这个时候孩子基础部分还不熟悉,直接上中档题或者难题,甚至,很多家长自己也不熟悉,直接一本书给孩子做,也不知道哪些是难题,哪些是简单题,既浪费孩子学习时间又打击孩子自信心。
不同阶段的孩子应该学哪些奥数内容?
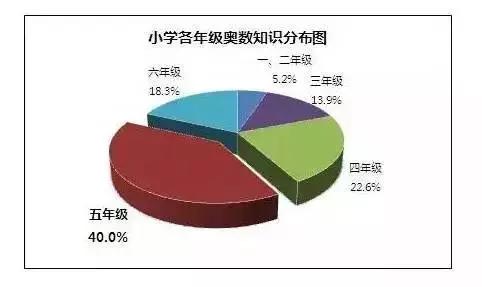
低龄化的奥数知识学习都以趣味知识为主,属于提前接触,大多数讲计算和基本数学概念和思维训练,简单的加减法计算技巧,图形转换等,相对容易些。
一二年级:
1.巧算与速算:
寻找到一定的规律,化繁为简,那么学生一定能够增强学习数学的信心,提高学习数学的兴趣。另外,计算与速算是各种后续问题学习的基础。学好数学,首先就要过计算这关。
2.学习简单的枚举法:
用数数这种更为直观的方式,将复杂抽象的问题形象化,便于孩子们理解。将抽象问题形象化,引导孩子去主动思考。
三四年级:
这个时期是奥数思维形成的关键时期,是学奥数的黄金时段,孩子的计算能力,认知能力,逻辑分析能力会有很大的提高,学习内容的难度和广度有所增加,各种竞赛任务和招生考试的成绩重要性大大增加, 是斩获各种杯赛、竞赛荣誉的关键时期。
1. 运用运算定律及性质速算与巧算:
能否又快又准的算出答案,是历年数学竞赛考察的一个基本点,要加强加法与乘法运算定律,其中应用乘法分配率是竞赛中考察巧算的一大重点;除此之外,竞赛中还时常考察带符号“搬家”与添括号/去括号这两种通过改变运算顺序进而简便运算的思路。例如:17×5+17×7+13×5+13×7这种技巧性试题。
重点题型有多位数的计算,小数的基本运算,小数的简便运算等。其中,多位数的计算主要以通过缩放讲多位数凑成各位数全是9的多位数,再利用乘法的分配率进行计算。重点在于以基础计算为主,掌握各种简便运算技巧,提高准确度和速度。
2. 理解假设思想解决鸡兔同笼问题:
鸡兔同笼问题源于我国1500年前左右的伟大数学著作《孙子算经》,这一类问题要求孩子要有假设思想,思路要很清晰。
3. 平均数应用题:
“平均数”这个数学概念在同学们的日常学习和生活中经常用到。如计算全班同学的数学“平均成绩”,同学与爸爸妈妈三个人的“平均年龄”等等,都是会经常碰到的求平均数的问题。
4. 和差倍应用题:
为了弄清题目中两种量彼此间的关系,需要孩子学习使用画线段图的方法以线段的相对长度来表示两种量间的关系,找到解题的途径。
和倍问题是已知大小两个数的和与它们的倍数关系,求大小两个数的应用题,一般可应用公式:数量和÷对应的倍数和=“1”倍量;
差倍问题就是已知大小两个数的差和它们的倍数关系,求大小两个数的应用题,一般可应用公式:数量差÷对应的倍数差=“1”倍量;
和差问题是已知大小两个数的和与两个数的差,求大小两个数的应用题一般可应用公式:大数=(数量和+数量差)÷2,小数=(数量和-数量差)÷2。
5. 行程问题:
行程问题要掌握以下各类的问题:相遇问题、追及问题、火车相遇问题、流水行船问题、多次相遇问题等。要求孩子对基本的相遇问题和追及问题有非常深刻的了解,在学习过程中经常有同学到六年级了对于追及问题中两个人所走的时间是否相等还经常容易出错。
6. 排列组合:
排列组合是对初期所学的加法原理和乘法原理两讲的一个升华。需要孩子在排列组合中首先要对排列组合的概念、排列数与组合数的计算、排列与组合的区别等有很好的理解,尤其是排列和组合的区分上,需要对一些经典例题的掌握从而来理解排列和组合的区别。
7. 几何计数与周期性问题:
几何计数和周期性问题也是各大竞赛和入学考试常见题型,尤其是很多综合题同时包含数论和周期性问题的相关知识点,是竞赛和备考的重中之重。尤其是吧周期性问题常和等差数列、数论结合在一起,孩子在做题题时经常容易出错,需要在这方面的加大做题量。
五六年级:
五六年级这个阶段的奥数学习应该有更强的针对性,针对孩子的实际情况和目标选择合适的班型。从最近的一些学校的考试可以看出一个趋势,就是题量大,时间段,对于单位时间内的做题效率有很高的要求,这个效率体现在两个方面,就是速度和正确率。
1. 递推方法:
递推方法就是从最简单的情况入手,通过处理简单的问题,我们可以从中得到规律或者诀窍,从而来解决复杂的问题。比如说:平面上2008条直线最多有几个交点?同学们第一眼看到这个问题时,肯定会想画2008条直线相交然后再数交点个数,那该是多麻烦啊!其实我们可以先来解决简单点的情况,分别找到1条、2条、3条、……以此类推,这些直线有多少个交点就会出现一个规律。
2.行程问题:
这个时期的奥数行程问题可以细分为:基本行程(单个物体)、平均速度、相遇、追及、流水行船、火车过桥、火车错车、钟表问题、环形线路上行程等等。只要掌握每个小类型中的诀窍,形成一种分析思路,复杂的行程问题也无非是这些类型的变形而已。
3.数论问题:
数论是五年级的核心知识,要解决抽象而又杂乱的的数论问题,首先得掌握数论的基本知识:数的奇偶性、约数(现在叫因数)、倍数、公约数及最大公约数、公倍数及最小公倍数、质数、合数、分解质因数、整除、余数及同余等。这些基本知识点里会出一些数论综合试题。
4.有抽屉原理:
生活中有很多有趣的事情,比如说:把4个苹果放到3个抽屉里,无论你怎么放,总有某个抽屉里至少有2个苹果,这就是抽屉原理。
5.图形面积计算:
求图形的面积一直是奥数中的一个难点,对于这类题要掌握好各种基本图形的面积计算公式,也必须熟记一些重要结论:比如三角形的等积变形、勾股定理、梯形中蝴蝶翅膀原理、相似三角形中边与面积的关系。
6.分数百分数问题,比和比例:
这些重点内容,在历年各个学校测试中所占比例非常高。
7.行程问题:
常常作为压轴题出现,是应用题里最重要的内容,综合考察孩子对比例,方程的运用以及分析复杂问题的能力,所以,重点应该掌握以下内容:
路程速度时间三个量之间的比例关系
用比例的方法分析解决一般的行程问题
重点是学会如何去分析一个复杂的题目
8.几何问题:
几何问题是各个学校考察的重点内容,具体的平面几何如直线形问题和圆与扇形;立体几何里分为表面积和体积两大部分内容。重点内容包括:等积变换及面积中比例的应用;与圆和扇形的周长面积相关的几何问题,处理不规则图形问题的相关方法;立体图形面积:染色问题、切面问题、投影法、切挖问题;立体图形体积:简单体积求解、体积变换、浸泡问题。
学好数学的方法
介绍数学学习方法的书就直接说:“学习的时候要开动脑筋。”“运算能力一定要好。”“理解比死记硬背重要得多。”“务必打好基础。”但是如果一旦问道:“这样啊!那么以我的水平,用这本辅导书,应该怎样去学呢?”他们就理科哑口无言了。
即使问数学学得不错的朋友,他们也只能支支吾吾的说“这个啊!好好努力的就行了吧!”话倒是没错,但这个回答对现实却一点帮助也没有。在我们这个以考试为评价尺度的现实中,这样的回答能有什么作用呢?
经过我们长期对学生进行辅导的过程中,精力过种种失败成功后,我们回忆自己的学习方法,留心观察我们教的学生们,以及多处实践,渐渐地,经过不停的研究,和教学过程中不断的完善,我们终于总结了一套在很多学生身上都去的了良好效果的学习数学比较有效的方法。
我所说的学习方法是指利用每个人手头上都有的教材(如教科书、辅导书、练习册)将数学实力在提高一个等级的方法。
只要按照我们总结的学习方法去学习,不管是什么辅导书,只需要学习两边就能完全掌握;不管遇到什么题目,都能从容的解答出来。
分析数学成绩不好的原因,找出对应方法
基础差:了解自己最根究低找到自己不会的最基础的地方,不要怕麻烦逐个击破。
太贪心:从基本概念公式学起,抓基础不盲目做难题。
不整理: ①整理题目特点和解题方法,让学过内容再次遇到很容易想起来②把一个单元中的题目按知识点集中到一起,让题目一目了然
没计划:按自己的实际情况合理安排学习计划
拖拉马虎:培养好的学习习惯