六年级奥数试题及答案汇总：最大问题

一、六年级奥数题及答案：最大数

1.从甲地到乙地原来每隔45米要装一根电线杆，加上两端的两根，一共有53根电线杆，现在改成每隔60米装一根电线杆，除两端的两根不需要移动外，中途还有多少根不必移动?

2.由1，3，4，5，7，8这六个数字所组成的六位数中，能被11整除的最大的数是多少?

答案与解析：

1.解答：45与60的最小公倍数是180，因此每隔180米的电线柑不用移动。甲乙两地之间距离为(53-1)×45=2340，因此有2340÷180+1=14根不用移动。

2.解答：数字和为1+3+4+5+7+8=28，因此奇数位与偶数位的数字和之差可以为0或22。如果是0，那么奇数为与偶数位数字和都是14，最大为875413。如果是22，那么奇数位与偶数位数字和分别为25和3，显然不成立。因此最大为875413。

二、1、

2、从0，1，2，……，9这10个数中取出3个数，使其和是不小于10的偶数，不同的取法共有多少种?

答案与解析：1、

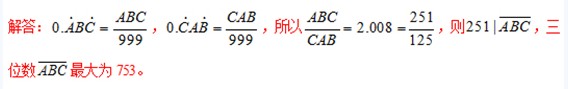
2、解答：从5个偶数中取出3个数，共有10种取法;取2个奇数，1个偶数，有50种取法，故和为偶数的不同取法有60种。

在这60种取法中，3数之和小于10的有：{0，1，3}、{0，1，5}、{0，1，7}、{0，2，4}、{0，2，6}、{0，3，5}、{1，2，3}、{1，2，5}、{1，3，4}共9种

综上可知满足要求的不同取法有51种。

三、十个不同的正整数的平均值是10，则这十个数的最大数的最大值是()

答案与解析：

分析：因为这个十个不同正整数的平均值是10，要使其中最大的正整数最大;即其余九个数大小是最小的正整数，即1、2、3、4、5、6、7、8、9、因此这十个数的最大数的最大值是10×10-1-2-3-4-5-6-7-8-9=55.

解：因为要使其中最大的正整数最大;即其余九个数大小是最小的正整数，即1、2、3、4、5、6、7、8、9;

所以这十个数的最大数的最大值是：10×10-1-2-3-4-5-6-7-8-9=55.

答：这十个数的最大数的最大值是55，

故答案为：55.

点评：根据题意要“使其中最大的正整数最大”;得出其余九个数大小是最小的正整数，即1、2、3、4、5、6、7、8、9是解答此题的关键.