动手学数学之三十一（推销员的旅程问题）

有些时候，我们必须去很多不同的地方办事，然后回到原出发点，所以我们通常想要找到最短的路径．这类问题被称为推销员的旅程问题，因为这是推销员在工作中最常遇到的问题．

然而，这也是许多人所要解决的问题，例如：

(1)油罐车的驾驶员必须将汽油运至各个加油站．

(2)运牛奶的卡车司机必须开车去分散在各地的农场．

(3)一位游客想要到剑桥、斯坦福、爱丁堡、朴利茅斯与巨石柱群等地旅游．

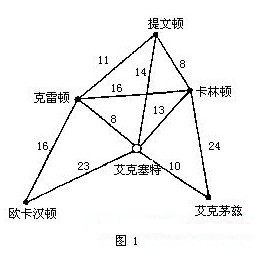
化妆品推销员李文黛小姐欲访问图1中的每个小镇，去推销新产品，她打算由艾克塞特出发．地图上所标示的数字为两小镇之间的距离，如果出发点与终点皆在艾克塞特的话，则最短的路径是怎样的？

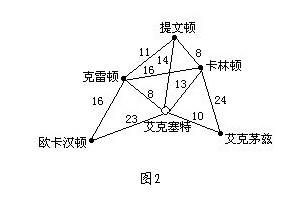
解决此种问题较常用的方法为最近城市法．此方法是先前往距离起点艾克塞特最近的城镇克雷顿，然后再去最靠近克雷顿且尚未到过的城镇，依此类推．用这种方法可得出如图2所示的解．在此图中我们先走完一路径：艾克塞特→克雷顿→提文顿→卡林顿→艾克茅兹→艾克塞特，然后再走另一路径：艾克塞特→欧卡汉顿→艾克塞特．

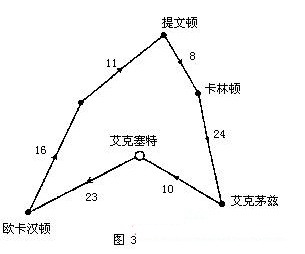
你自己可能会发现如图3的解，此解的基本想法是将所有的城镇连成一个回路，所得出的答案为92英里．这个答案虽比前面的好得多了，但还不是最佳的解．最佳路径的里程只有91英里，你能找到吗？

假设现在李文黛又把汉尼顿列入她的行程之中(图4)，那么整个行程的最短路径为何(其出发点与终点仍为艾克塞特)？如果将出发点及终点皆改为卡林顿，会不会使整个行程变得较短呢？如果以不同的城镇为起点与终点，是否会影响总里程数呢？

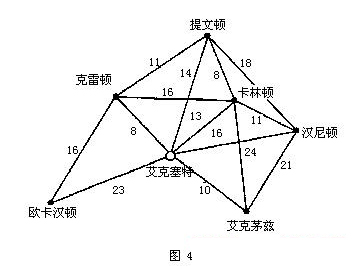
如果李文黛的起点及终点可以不同，那么她该选择哪两个城镇为起点及终点，以使整个行程为最短？

数学家们曾耗费许多心思以解决这类问题，但是到目前为止尚未成功．但他们知道在最短的路径中，各条路线彼此不可交错．然而当他们发现正确的解法时，若城镇的数目增加很多，又不适用了．他们甚至采用了先进的大型电脑作为辅助工具，利用系统的“试误法”．要找到“好”的解(可能并不是最好的)，方法很多，但如果有人能找到一个直接且快速的方法求得最佳路径，肯定会声名大噪！

英国每年都有成千上万的青少年会参加著名的“十岩探险”，整个探险路线包括要探访的所有著名的岩石地带(花岗岩通常露在山丘之顶)，如地图中所显示的地点(图5)．在正式探险之前

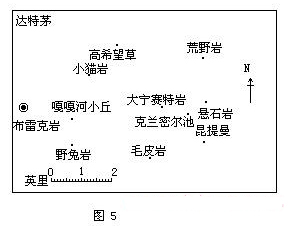
几个月的周末，经常可以发现一些人在当地进行野外训练．某个周末，一支队伍先在地图上规划路线，他们打算由布雷克岩出发，然后经过图上标示的所有地方再回到出发点，他们希望尽可能找到最短的路径．

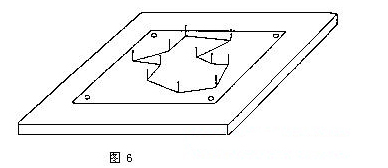
解决此类问题的一个方法是先将地图描在纸上，并将纸固定在画板上．然后将钉子钉在每一个要探访的地方，再用不同长度、不同颜色的棉线来标出可能的路径，其中最短的线段当然就对应于最佳的路径(图6)．

你也可以利用地图来研究一下这类问题．