二年级奥数知识点：逆序推理法

逆序推理法，也叫逆推法或倒推法.简单说，就是调过头来往回想.

例1 老师心中想了一个数，对他的学生说：“给这个数加上9，再取和的一半应是5.”他叫学生们把这个数算出来.你会算吗?

解：用逆推法求解，就是这样想：因为老师想的数加上9后之和的一半是5，那么和就应是 5×2=10;再往前逆推，在没有加上9之前应是10-9=1，这就是老师心中想的数.

让我们再从另一种思路去想：

首先，把老师想的数用□代表，顺着题意列式应有：

(□+9)÷2=5，我们可以叫它做顺序式.

然后，再把前面的逆推过程写成算式，就应有：

5×2-9=，“1”就是方框所代表的数，所以把它写在方框里.我们可以把这个算式叫做逆序式.把两式进行对照比较(如下图如示)可见：

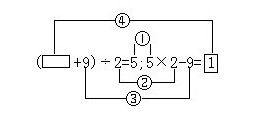
①顺序的运算结果(或最后结论)是逆序式的已知数据(或起始条件);

②顺序式中除以2变为逆序式中乘以2;

③顺序式中加上9变为逆序式中减去9;

④顺序式中起始未知数变为逆序式中最后运算结果;

总之，逆序式恰为顺序式的逆运算.

这就是逆推法的由来和实质.

例2 某数加上6，乘以6，减去6，除以6，最后结果等于6.问这个数是几?

解：依题意，写出顺序式，再接着写出逆序式，

[(某数+6)×6-6]÷6=6…顺序式

(6×6+6)÷6-6=某数…逆序式

经计算可知“某数”=1.

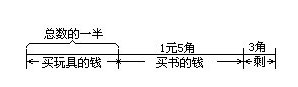
例3 小勇拿了妈妈给的零花钱去买东西.他先用这些钱的一半买了玩具，之后又买了1元5角钱的小人书，最后还剩下3角钱.你知道妈妈给小勇多少钱吗?

解：可以这样倒着想：小勇最后剩下3角钱，在买书之前的钱应是3角+1元5角=1元8角.这个数目是他买玩具后剩下的，买玩具前的钱数应当是：1元8角×2=3元6角.这就是妈妈给他的钱数.

若画出下面的图就更清楚了.

例4 小亮拿着1包糖，遇见好朋友A，分给了他一半;过一会又遇见好朋友B，把剩下的糖的一半分给了他;后来又遇到了好朋友C，把这时手中所剩下的糖的一半又分给了C，这时他自己手里只有一块了.问在没有分给A以前，小亮那包糖有几块?

解：采用逆推法--从最后结果往前倒着推算.小亮最后手里只剩下一块糖，这是分给C一半后所剩的数，则知遇见C之前小亮有糖：

1×2=2(块).

同理，遇到B之前有糖：2×2=4(块).

遇到A之前有糖：4×2=8(块).

即小亮未给小朋友前，那包糖应有8块.

例5 农妇卖蛋，第一次卖掉篮中的一半又1个，第二次又卖掉剩下的一半又1个，这时篮中还剩1个.问原来篮中有蛋几个?

解：

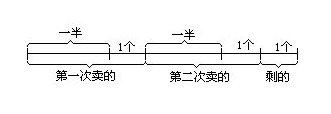
逆推：篮中最后(即第二次卖后)剩1个;

第二次卖前篮中有(1+1)×2=4个;

第一次卖前篮中有(4+1)×2=10个;

即篮中有10个蛋.

例6 某池中的睡莲所遮盖的面积，每天扩大1倍，20天恰好遮住整个水池，问若只遮住水池的一半需要多少天?

解：倒着想.若是今天睡莲把整个池面遮满了，那么昨天睡莲只遮住了水面的一半.今天是第20天，昨天就是第19天，也就是说睡莲遮住一半池面需19天.

例7 文化用品店新到一批日记本，上一周售出本数比总数的一半少12本;这一周售出的本数比所剩的一半多12本;结果还有19本.问这批日记本有多少?

解：

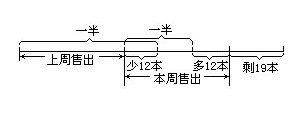
由图上可见本周未售出时的一半是：

19+12=31(本);

本周未售出时的总数是：

31×2=62(本);

总数的一半是：

62-12=50(本);

总本数是：

50×2=100(本).

列出综合算式：

[(19+12)×2-12]×2=100(本).

答：这批日记本共有100本.

例8 现有一堆棋子，把它分成三等份后还剩一颗;取出其中的两份又分成三等份后还剩一颗;再取出其中的两份再分成三等份后还剩一颗.问原来至少有多少颗棋子?

解：题中有“至少”这一条.

用逆推法从最后的最少棋子情况逆推.先画线段图依次表示分棋子的过程，见下图：

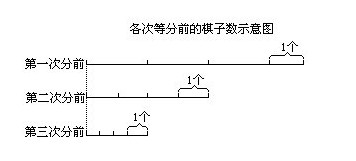
假设第三次分时，三等份中每分是1个棋子(最少)，

则此次分前应是3+1=4个;4÷2=2，则第二次分前应是2×3+1=7个，注意7是奇数(第二次分前的棋子是第一次分后的两份，应是偶数所以不应是7，可见前面假设不对).

再假设第三次分时每等份是2个棋子，也不行.

又假设第三次分时每等份是3个棋子，则有

3×3+1=10;

10÷2=5，5×3+1=16;

16÷2=8，8×3+1=25;

∴原来有棋子至少是25个.