二年级奥数知识点：猜猜凑凑

有些数学题可以用猜猜凑凑的方法求出答案.猜，很难一次猜中;凑，也不一定凑得准.那不要紧，再猜再凑，对于比较简单的问题，最后总能凑出答案来.

数学家说，猜猜凑凑也是一种数学方法，它的正式的名字叫“尝试法”.有时，它还是一种极为有效的方法，数学上的有些重大的发现往往都是大数学家们大胆地猜出来的.

猜，要大胆;凑，要细心.要知道猜的对不对，还要根据题目中的条件进行检验.

例1 小明心中想到三个数，这三个数的和等于这三个数的积，你知道小明想的三个数都是什么吗?

解：猜——小明想的三个数是1、2、3.

检验：1+2+3=6

1×2×3=6

所以 1+2+3=1×2×3

对了!

解：猜——由△+□=3可猜△=1，□=2;

又由△+○=4可猜△=1，○=3;

检验：□+○=2+3=5，对了!

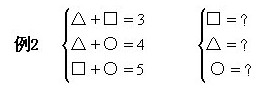
所以△=1，□=2，○=3.

例3 一些老人去赶集，买了一堆大鸭梨，一人一梨多一梨，一人两梨少两梨，问几个老人几个梨?

解：猜——可以先从小数猜起.2个老人3个梨.检验：2个老人3个梨符合一人一梨多一梨的条件.

但是不是符合另一个条件呢?

先看：若一人分两个梨，2个老人就需要有4个梨，因为假设3个梨，这样就会还少4-3=1个梨，这不符合少两梨的条件.

再猜：若是3个老人4个梨呢?显然这符合第一个条件.再看第二个条件是不是也符合呢?若是一个老人分2个梨，3个老人就需要有6个梨，假设有4个梨，这样就少6-4=2个梨，对了!

所以最后答案就是3个老人4个梨.

例4 100个和尚分100个馒头，大和尚每人分3个馒头，小和尚3人分1个馒头，恰好分完.问大和尚、小和尚各多少人?

解：这是一道古代的算题.

猜——若是大和尚33人，就要分3×33=99个馒头，还剩100-99=1(个)馒头，分给3个小和尚，这样和尚总人数为33+3=36人，与已知有100个和尚不符，不对!

大和尚的人数减少些.若是有30个大和尚，分3×30=90个馒头，还剩10个馒头，可以分给3×10=30个小和尚，这样和尚总数是30+30=60人.

还必须减少大和尚的人数.若是有25个大和尚，分3×25=75个馒头，还剩100-75=25个馒头，可以分给3×25=75个小和尚.这样和尚总数是25+75=100人，对了.

所以答案是大和尚25人，小和尚75人.

例5 甲、乙、丙三个小朋友在操场跑步.甲2分钟跑一圈，乙3分钟跑一圈，丙5分钟跑一圈.如果他们三人同时从同一起点起跑，问多少分钟后他们三人再次相遇?

解：猜与凑.

先猜过6分钟后，甲跑了3圈，乙跑了2圈，他们在起跑点又相遇了.再看丙是否与他俩相遇呢?丙5分钟跑一圈，6分钟跑了1圈多一点，错过了，丙没能与甲、乙相遇在一起.

若再过6分钟，即12分钟后，甲和乙又相遇了.但是丙还不能与甲、乙相遇;因为：

12÷5=2(圈)……2

即丙跑了2圈又多一些.

这样，已看出一个规律来了，能够估计出若起跑后经过5个6分钟，即6×5=30分钟，这时丙跑了30÷5=6圈整，这样丙就能够与甲、乙相遇了.

例6 有人问孩子年龄，回答说：“比父亲的岁数的一半少9岁”.

又问父亲年龄，回答说：“比孩子的岁数的3倍多3岁”.求父亲和孩子的年龄各是多少岁?

解：猜猜凑凑——要找到对题中的两句话都适合的年龄.先猜父亲40岁，

则儿子年龄是：40÷2-9=20-9=11(岁)

检验父龄：

11×3+3=33+3=36岁，不对!

再猜父亲42岁，

则儿子：42÷2-9=21-9=12(岁)

检验父龄：

12×3+3=36+3=39(岁)，不对!

再猜父亲44岁，

则儿子：44÷2-9=22-9=13岁

检验父龄：

13×3+3=39+3=42岁，不对!

再猜父亲46岁，

则儿子：46÷2-9=23-9=14岁

检验父龄：

14×3+3=42+3=45岁，不对!

再猜父亲48岁，

则儿子：48÷2-9=24-9=15岁

检验父龄：

15×3+3=45+3=48岁，对了!

所以答案是：父亲年龄48岁，儿子年龄15岁.