二年级奥数考虑所有可能情况（一）

有些数学题，要求把符合条件的算式或得数全部找出来；若漏掉一个，答案就不对.做这种题，特别强调有秩序的思考.

例1 从2个5分硬币、5个2分硬币、10个1分硬币中，拿出1角钱来，有多少种不同的拿法？

解：找出所有不同的搭配情况，共10种见下表.

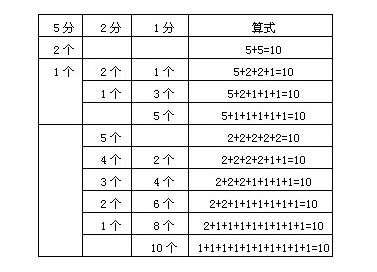
例2 5个茶杯的价钱分别是9角、8角、6角、4角和3角，3个茶盘的价钱分别是7角、5角和2角；如果一个茶杯配一个茶盘，一共可以配成多少种不同价钱的茶具？

解：采取“笨”办法进行搭配.先把各种不同价钱的茶杯都配上一个7角钱的茶盘，得出不同价钱的茶具如下：

将这些茶杯与5角钱的茶盘搭配，又可得出一些不同价钱的茶具，但要注意去掉那些与前面相同的价钱：

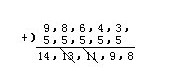
再将这些茶杯与2角钱的茶盘搭配，同时去掉那些与前面相同的价钱：

最后数一数，共有10种不同价钱的茶具.这些价钱是1元6角，1元5角，1元4角，1元3角，1元1角，1元，9角，8角，6角，5角.

例3 将无法区分的7个苹果放在三个同样的盘子里，允许有的盘子空着不放.问共有多少种不同的放法？

解：用数字代表盘子里的苹果数，用由3个数字组成的数组表示不同的放置方式.如（7，0，0）表示：一个盘子里放7个苹果，而另外两个盘子里都空着不放.各种可能的放置情况如下：

（7，0，0）

（6，1，0）

（5，2，0），（5，1，1）

（4，3，0），（4，2，1）

（3，3，1），（3，2，2）

数一数，共有8种不同的放法.

例4 把一个整数表示成若干个小于它的自然数之和，通常叫做整数的分拆.问整数4有多少种不同的分拆方式？

解：分拆时，使自然数按由大到小的顺序出现.可以看出，共有4种不同的分拆方式：

4=3+1

4=2+2

4=2+1+1

4=1+1+1+1.

例5 邮局门前共有5级台阶.若规定一步只能登上一级或两级，问上这个台阶共有多少种不同的上法？

解：如图10—1，同时用数组表示不同的上法.

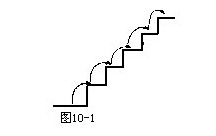
（1，1，1，1，1）表示每步只上一级，只有1种上法.

见图10—2，①（2，1，1，1）②（1，2，1，1）

③（1，1，2，1）④（1，1，1，2）

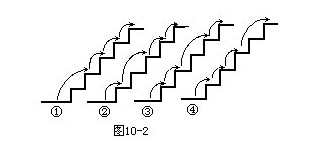
表示有一步上两个台阶，其他几步都各上一个台阶，共有四种上法.

见图10—3，①（2，2，1），②（1，2，2），

③（2，1，2）.

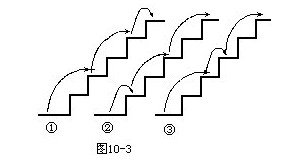
表示有两步各上两个台阶，有一步上一个台阶，这种上法共有3种.因此，上台阶共有1+4+3=8种不同的上法.